The research team led by Liu Zhengyou, Qiu Chunyin and Ke Manzhu, from the School of Physics and Technology of Wuhan University, has successively published two research achievements in the field of topological acoustics. One paper entitled "Observation of quadratic Weyl points and double-helicoid arcs" was published in Nature Communications. Another paper titled "Symmetry-enforced three-dimensional Dirac phononic crystals" was published in Light: Science & Applications.
Wuhan University is the first signature unit of the paper "Observation of quadratic Weyl points and double-helicoid arcs". Postdoctoral fellow He Hailong is the first author, and Prof. Qiu Chunyin and Prof. Liu Zhengyou are co-corresponding authors. Collaborators in this work also include Cai Xiangxi, a doctoral student in WHU, Prof. Xiao Meng and Prof. Ke Manzhu in WHU, and Prof. Zhang Fan in the University of Texas at Dallas in the United States. These two studies were supported by National Key Research and Development Project, and Major Program of the National Natural Science Foundation of China and other funds.
In recent years, a great number of researches have been conducted on topological semimetals, represented by Dirac semimetals and Weir semimetals (respectively characterized by isolated quadruple and double linear degeneracy in the three-dimensional Brillouin zone), which are analogs of high-energy physics. Recently, "unconventional quasi-particles" that surpass the above high-energy analogs have attracted great attention from condensed matter physics and materials science community.
The research reports an experimental observation of the quadratic Weyl points and its corresponding double-helicoid surface arcs by a three-dimensional chiral metacrystal of sound waves. Markedly different from such newly observed unconventional quasiparticles as the spin-1 Weyl points and the charge-2 Dirac points featuring respectively threefold and fourfold band crossings, the quadratic Weyl points identified here are simply twofold degenerate, and the dispersions around them are quadratic in two directions and linear in the third one(as shown in Figure 1). Besides these abnormal dispersion characteristics, the research further unveils the exotic double-helicoid surface arcs that emanate from a projected quadratic Weyl point and terminate at two projected conventional Weyl points. This unique global surface connectivity provides conclusive evidence for the double topological charges of such unconventional topological nodes (as shown in Figure 2).

Figure1: (a) A partially enlarged view of four different Weyl points in the acoustic metacrystal, where the simply twofold degenerate points of Γ and A are quadratic Weyl points, and the others are conventional Weyl points. (b-d) The corresponding experimental proof.
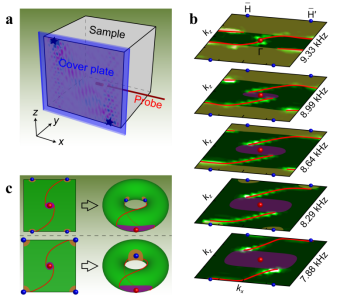
Figure2: Experimental verification of the double-helicoid surface arcs.
The paper "Symmetry-enforced three-dimensional Dirac phononic crystals" is published with Wuhan University as its unique signature unit. Cai Xiangxi, a doctoral student in the School of Physics and Technology, is the first author. Postdoctor Ye Liping and Prof. Liu Zhengyou are co-corresponding authors. Collaborators in this work also include Prof. Qiu Chunyin, Prof. Xiao Meng, Prof. Yu Rui, and Prof. Ke Manzhu.
It has become a vital goal in fundamental physics and material science to explore new topological states of matter. A three-dimensional (3D) Dirac semimetal (DSM), accommodating many exotic transport properties such as anomalous magnetoresistance and ultrahigh mobility, is an exceptional platform for exploring topological phase transitions and other novel topological quantum states. A DSM phase may appear accidentally at the quantum transition between normal and topological insulators. The approach to such a single critical point demands the fine-tuning of the alloy’s chemical composition, which is difficult to achieve experimentally. Also, 3D DSMs can emerge without fine-tuning parameters and are distinguished into two classes. The first one, already realized in Na3Bi and Cd3As2, occurs due to band inversion. The Dirac points, lying on the generic momenta of a specific rotation symmetry axis, always come in pairs and could be eliminated by their merger and pairwise annihilation through the continuous tuning of parameters that preserve the symmetry of the system. The second class features Dirac points that are pinned stably to discrete high-symmetry points on the surface of the Brillouin zone (BZ). Unlike the first class of DSMs, the occurrence of Dirac points is unavoidable in the nonsymmorphic space group of the material, which cannot be removed without changing the crystal symmetry. Although some solid-state candidate materials have been proposed, symmetry-enforced 3D DSMs have never been experimentally realized because of the great challenge in synthesizing materials. Recently, numerous distinct topological states have been demonstrated in classical wave systems, such as photonic crystals, which facilitates further exploration of topological physics in a fully controllable manner.
Here, researchers constructed and reported an experimental realization of a 3D phononic crystal that hosts symmetry-enforced Dirac points at the BZ corners(as shown in Figure 3). In addition to the Dirac points identified directly by angle-resolved transmission measurements (as shown in Figure 4), highly intricate quadhelicoid surface states are unveiled by the surface measurements and associated Fourier spectra (as shown in Figure 5). Specifically, the surface states are composed of four gaplessly crossed spiral branches and thus are strikingly different than the double Fermi arc surface states observed recently in electronic and photonic systems. Starting with this structure, one can design various interesting 3D acoustic topological states through symmetry reduction. It is noteworthy that here the dispersion around the Dirac point is isotropic, and thus, the macroscopic system can provide new opportunities for the study of relativistic physics and serve as a unique platform to simulate the application of acoustics.
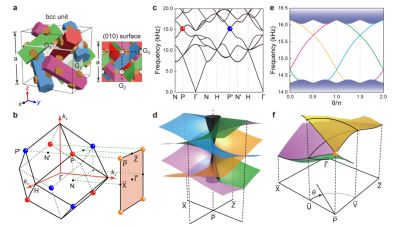
Figure3: Symmetry-enforced Dirac points and quad-helicoid topological surface states in a nonsymmorphic phononic crystal
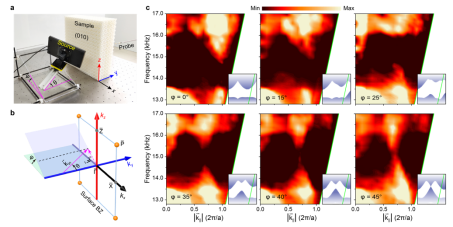
Figure4: Experimental identification of the symmetry-enforced Dirac points
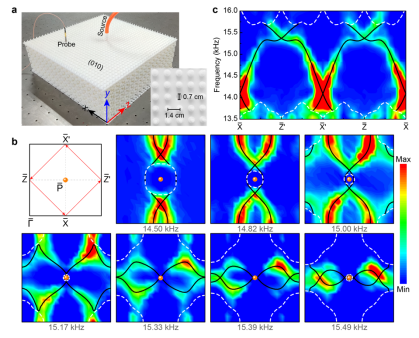
Figure5: Experimental observation of quad-helicoid topological surface states
Written by Zhang Yifei
Rewritten by Wang Anqi
Edited by: Wu Buer, Shen Yuxi and Hu Sijia